Introduction
In the world of engineering, a broad array of techniques and methodologies are utilized to evaluate and enhance the performance, durability, and efficiency of materials. Among these, Finite Element Analysis (FEA) and Poisson’s Ratio are two commonly implemented approaches. However, it is crucial to discern the disparities between these two methods to ensure their optimal application in various engineering contexts.
The focal point of this discourse will be the exploration of these two disparate techniques, particularly emphasizing the importance of comprehending their differences. A comprehensive understanding of these differences is instrumental in making informed decisions during the selection of an appropriate analysis method for various engineering scenarios. The aim is to equip engineers with the necessary knowledge to improve their ability to design and analyze Fiber Reinforced Polymers (FRP) and Composite Metal Hybrid structures with greater precision and efficacy.
As the journey into the depths of FEA and Poisson’s Ratio commences, it is hoped that readers will gain valuable insights and develop a more profound understanding of these techniques’ roles and applications in the field of engineering.
Understanding the Basics
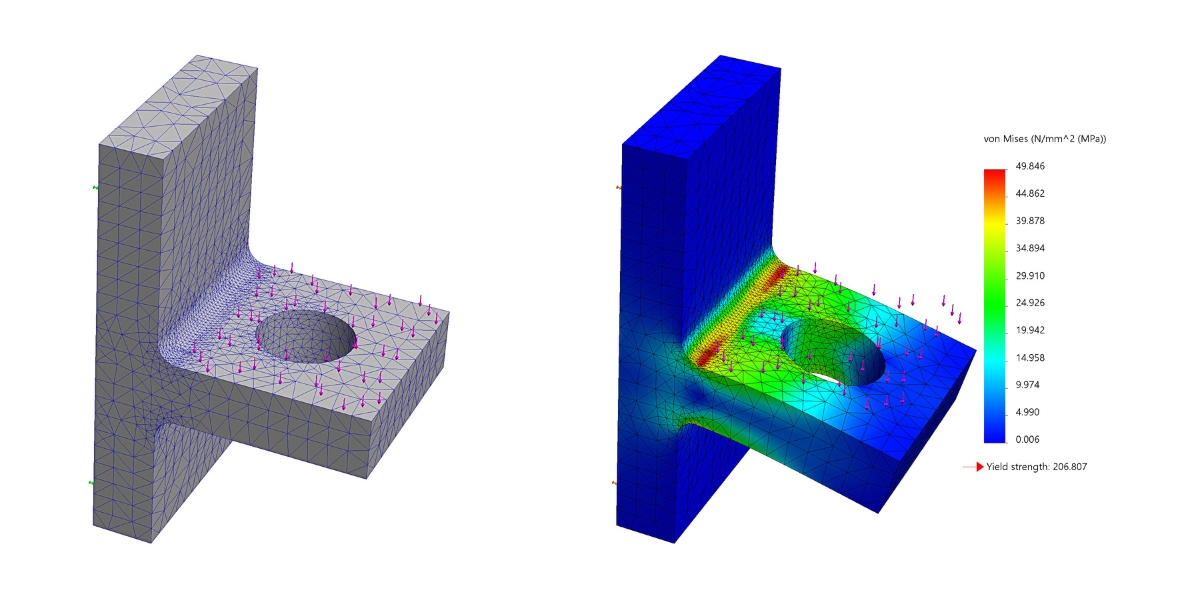
In the realm of engineering, Finite Element Analysis (FEA) is utilized as a sophisticated computational method. It enables the simulation of various physical phenomena based on the finite element method (FEM). FEA is employed for predicting how products react to real-world forces, such as heat, vibration, fluid flow, and other physical effects. The strength and motion of a part or a product can be tested and analyzed using FEA, which can accurately determine whether a product will break, wear out, or work as intended.
Example of Finite Element Analysis (FEA)
Poisson’s Ratio, on the other hand, is a measure of the deformation behavior of materials. Named after Simeon Poisson, it is defined as the negative ratio of transverse to axial strain. When a material is compressed or expanded in one direction, it usually tends to expand or contract in the other two directions. Poisson’s Ratio measures this predictable deformation effect.
In the context of Fiber Reinforced Polymers (FRP) and Composite Metal Hybrid structures, these two techniques play significant roles. FRPs are composite materials made of a polymer matrix reinforced with fibers. They are known for their high strength-to-weight ratio and excellent corrosion resistance. On the other hand, Composite Metal Hybrid structures combine the advantages of metal and composite materials, offering superior performance in terms of weight, strength, and durability. Both FEA and Poisson’s Ratio can be used to analyze and design these materials, but each method has its limitations and advantages. A deeper understanding of these techniques will assist engineers in making informed decisions and optimizing their designs.
The Limitations of Using Poisson’s Ratio in Engineering
The utilization of Poisson’s Ratio in the field of engineering has traditionally been an integral part. This ratio, which is the negative ratio of transverse to axial strain, has been relied upon in the prediction of deformation behavior of materials under load. It is a dimensionless constant that plays a crucial role in the analysis and design of structures.
However, it is essential to shed light on the limitations and potential issues associated with an over-reliance on Poisson’s Ratio. One of the most notable limitations of this method is its assumption of material isotropy. In reality, most materials exhibit some degree of anisotropy, which can significantly affect their mechanical behavior. Therefore, the use of Poisson’s Ratio for such materials may lead to inaccurate predictions.
In addition, Poisson’s Ratio does not take into account the effects of temperature, strain rate, or other environmental factors. These factors can significantly influence the mechanical properties of materials, leading to deviations from the predictions made using Poisson’s Ratio.
Furthermore, Poisson’s Ratio is often determined experimentally, meaning that it is subject to experimental errors. Any inaccuracies in the measurement of strains can lead to significant errors in the calculated value of Poisson’s Ratio, affecting the accuracy of subsequent analyses and designs.
Lastly, the use of Poisson’s Ratio assumes linear elastic behavior. However, many materials exhibit non-linear behavior under certain conditions, and thus, the application of Poisson’s Ratio may not provide a comprehensive understanding of the material’s response.
These limitations underscore the importance of using a more holistic and comprehensive approach when analyzing and designing structures. While Poisson’s Ratio can provide valuable insights, it should be complemented with other methods, such as Finite Element Analysis, to ensure a more accurate and reliable outcome.
The Advantages of Using FEA in Engineering
In the field of engineering, Finite Element Analysis (FEA) is applied extensively as it provides a comprehensive approach to predicting how a product will react under real-world conditions. It allows engineers to virtually test and analyze the behavior of structures and materials under various conditions such as mechanical stress, strain, heat, vibration, and other physical effects.
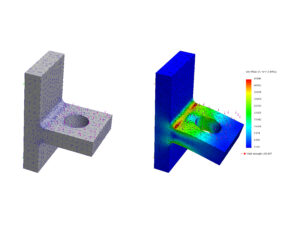
Several benefits and advantages are associated with the use of FEA. One of the primary advantages is its versatility. Unlike Poisson’s Ratio that assumes isotropic and linear behavior of materials, FEA can model complex material behaviors including non-linear, anisotropic, and time-dependent properties. This makes FEA a powerful tool for analyzing complex materials and structures, such as Fiber Reinforced Polymers and Composite Metal Hybrid structures.
Example of a Finite Element Analysis (FEA)
Another advantage is the ability of FEA to model complex geometries and boundary conditions. While Poisson’s Ratio is limited to simple geometrical shapes and uniform loads, FEA can handle complex shapes and varying load conditions, providing a more accurate representation of real-world scenarios.
FEA also allows for the optimization of designs before they are manufactured. By using FEA, potential design flaws can be identified and rectified in the design stage itself, thereby saving time, resources, and reducing the risk of failure.
Moreover, FEA provides detailed visualizations of the analyzed structure. It generates results that can show the distribution of stresses, displacements, and other physical quantities throughout the structure. This cannot be achieved through Poisson’s Ratio, which only provides a single value for the entire material or structure.
In conclusion, while Poisson’s Ratio has its value in engineering applications, the use of Finite Element Analysis offers a more comprehensive, versatile, and accurate method for the analysis and design of structures. It is a tool that is instrumental in ensuring reliability, optimizing designs, and enhancing the performance of products. Therefore, the importance of understanding and utilizing FEA in engineering cannot be overemphasized.
Conclusion
In this discussion on engineering materials, particularly Fiber-Reinforced Polymers (FRP) and Composite Metal Hybrids, we contrasted the utility of Poisson’s ratio with the capabilities of Finite Element Analysis (FEA).
While Poisson’s ratio offers a basic understanding of material deformation, it has limitations, especially when compared to FEA. Unlike FEA, Poisson’s ratio can’t account for complex geometries, multiple materials, or nonlinear behavior — factors often critical in advanced engineering contexts.
FEA provides a more comprehensive and nuanced understanding of materials under various conditions. It accommodates complexity in both material types and structural shapes, making it a more robust tool for FRP and Composite Metal Hybrid engineering.
In summary, although Poisson’s ratio has its place, FEA presents a more versatile and accurate approach for modern engineering applications, justifying its growing adoption in the field.
To learn more about FEA of composite metal hybrids (CMH™) visit our website or contact us today.
© 2023 Advanced Architectural Products